# Relation
Relation objects describe the relation between two competencies within a Competency Framework, allowing:
- Competencies to be organized into hierarchies
- Prerequisite relationships to be established
- Creation of equivalences across frameworks.
Relations in CASS exist outside of (but can be referenced within) competencies and frameworks, so that frameworks may reuse competencies and rearrange them in a different structure.
Relations can, therefore, represent a relationship between two competencies within the same framework or two competencies in separate frameworks. Relations can also be considered independent of a framework.
# Relation Types
Relations are directional and labeled. Let's look at the different types.
# Narrows
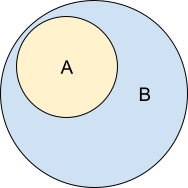
A Narrows B states that the entirety of the task in A is contained within B and that A helps describe B. This relation can also be stated as “A is a subcompetency of B”. With set theory we could say that “A is a subset of B”.
When presenting this relationship, it is useful to think of an indented list:
- B
- A
Example: Addition narrows Basic Arithmetic
# Requires

A Requires B describes a relation where it is necessary to hold the competency B before the competency A may be obtained. As opposed to a Narrows relation, A and B are logically distinct. B may be involved in the steps to complete A, but it does not help describe A.
When presenting this relationship, it is useful to consider a sequential checklist where all previous items must be completed before the current item.
- B
- A
Example: Multiplication requires Addition
# Equivalent
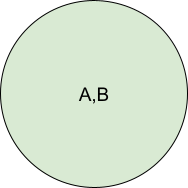
A is Equivalent to B describes a relation where two competencies represent the same capability in all aspects. The wording may be somewhat different, but there should be no distinction between these two competencies.
When presenting this relationship, it is useful to append additional names.
- A (also known as B)
- A (aka B)
Example: Addition is equivalent to Sums
# Related
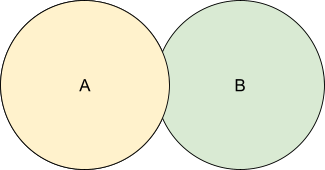
A is Related to B describes a relation where two competencies involve some degree of overlap such that interest in A may be followed by interest in B or visa versa. With set theory we could say that “there exists an intersection between A and B”.
When presenting this relationship, it may be useful to annote with “Did you mean” or “Related: ”, or augment them in search results.
- A
- Related:
- B
- Related:
Example: Division is related to Grouping
# Desires

A desires B describes a relation where B is not essential to the acquisition of A, but it may be desired, lightly assumed, or implied by the declaration of A.
When presenting this relationship, present it similarly to Requires, but ensure the individual knows it is optional.
- B (optional)
- A
Example: Multiplication desires Subtraction. (for some strategies)
# Is Enabled By
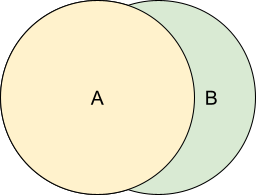
A is Enabled by B describes a relation where the acquisition of B speeds or makes more probable the acquisition of A.
When presenting this relationship, present it similar to Requires, but as a recommended option.
- B (recommended)
- A
Example: English Speaking enables English Writing
# Computational Complexity
There are several methods to consider when determining competence. Consider:
- Basic Arithmetic
- Addition
- Subtraction
- Multiplication
- Division
Addition, Subtraction, Multiplication, and Division all have a narrows relationship with Basic Arithmetic.
If a person holds all four sub-competencies of Basic Arithmetic, do they also implicitly hold Basic Arithmetic?
An optimistic strategy assumes that it is aware of all information about a particular competency. It would conclude that the person does hold Basic Arithmetic because Basic Arithmetic is only composed of its sub-competencies: Addition, Subtraction, Multiplication, and Division.
The pessimistic route presumes there may be additional unidentified information about a competency (such as undefined competencies) and could make no determination about Basic Arithmetic based on the holding of its four sub-competencies. (Note: However, a pessimistic process may conclude that that the person does NOT hold Basic Arithmetic if there is an explicit assertion that the person does not hold one of the subcompetencies.)
It is important to understand the possibilities and potential issues and to have a clearly defined goal as these relations are subject to interpretation. See Assertion Processing for further information.
# Creation
var c1 = new EcCompetency();
c1.generateId("https://dev.cassproject.org/api/");
c1.addOwner(EcIdentityManager.ids[0].ppk.toPk());
c1.name = "Competency 1";
var c2 = new EcCompetency();
c2.generateId("https://dev.cassproject.org/api/");
c2.addOwner(EcIdentityManager.ids[0].ppk.toPk());
c2.name = "Competency 2";
var r = new EcAlignment();
r.generateId("https://dev.cassproject.org/api/");
r.addOwner(EcIdentityManager.ids[0].ppk.toPk());
r.source = c1.shortId();
r.target = c2.shortId();
r.relationType = Relation.NARROWS;
// Don’t forget to save these objects!
# Adding a Relation to a Framework
f.addCompetency(c1.shortId());
f.addCompetency(c2.shortId());
f.addRelation(r.shortId());
// Don’t forget to save these objects!
# Save
EcAlignment has a helper method that validates expected fields before saving.
r.save(function() {}, function(error) {});
# Delete
EcAlignment has a helper method that deletes the alignment. This does NOT DELETE any objects referenced by the alignment.
r._delete(function(success){},function(failure){});
# Get
EcAlignment has a static helper method for retrieving an Alignment, automatically decrypting it, automatically encrypting it on save, and casting it to the EcAlignment object. The blocking version locks the thread while this occurs.
EcAlignment.get(
url,
function(framework) {},
function(error) {}
);
// Alternatively...
var r = await EcAlignment.get(url);
# Search
EcAlignment has a static helper method for searching for Alignments.
// Searches for alignments
EcAlignment.search(
repo,
null,
function(arrayOfEcAlignments) {},
function(error) {}
);
// Searches for up to 5000 alignments that originate from a competency.
EcAlignment.search(
repo,
`source:"${c.id}"`,
function(arrayOfEcAlignments) {},
function(error) {},
{size:5000}
);
